| Correct Answers: | |
| Wrong Answers: | |
| Unattempted: |
Question 1
A dice with faces marked is shown below:
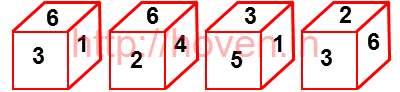
The face opposite to 3 is
Question 2
Which number will be on the face opposite to the face which contains 2 ?
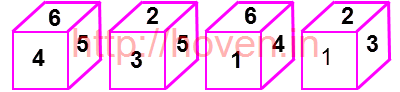
Question 3
Six cubes with their upper faces erased are as shown.
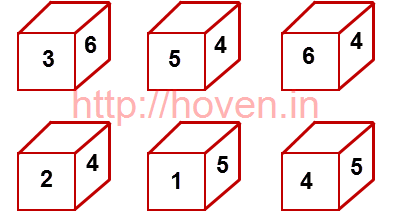
The sum of the numbers on the opposite faces is 7.
If odd numbered dice have even numbers on their top faces, then what would be the sum total of the numbers on the faces of these three dice ?
Ans: a
The odd numbered dice are 1, 3 and 5. Consider this deduction.
- Dice No.1: Face opposite 3 is 4 because 3 + 4 = 7. So 6 and 4 appear on the sides which means 2 is at the top.
- Dice No. 3: 6 and 4 are on the sides, so 2 must be at its top.
- Dice No. 5: The digit 2 should be opposite 5, and 6 should be opposite 1. This reveals 2 and 6, so 4 must be at the top of this dice.
The sum of numbers is 2 + 2 + 4 = 8.
Question 4
A dice has numbers 1, 2, 3, 4, 5 and 6 on its faces. Four positions of the dice are as shown below. The number on the face opposite to the face with number 6 is
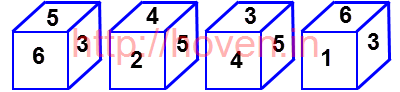
Question 5
Six cubes with their upper faces erased are as shown.
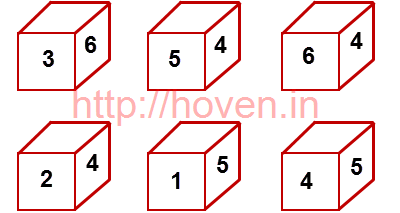
The sum of the numbers on the opposite faces is 7.
If the even numbered dice have odd numbers on their top faces and odd numbered dice have even numbers on their bottom faces, then what would be the sum of the numbers on the top faces of all the dice?
Ans: c
Since the sum of digits on opposite faces is 7, faces with odd digits would have even digits opposite them. Hence, the digits at the top of all these dice are odd. Let's deduce them. We have been given that the sum of the digits on each of the opposite faces is 7. To find the odd number at the top, we should prove that two out of the three odd numbers 1, 3 and 5 appear on the sides. Then the third will automatically be on the top.
- Dice 1: The number opposite 6 is 1, and the number 3 is already visible, so the number at the top is 5.
- Dice 2: The number opposite 4 is 3, so the number at its top is 1.
- Dice 3: The number opposite 6 is 1, the number opposite 4 is 3, so the number at the top is 5.
- Dice 4: By the same logic as above, the number at the top is 1.
- Dice 5: By the same logic as above, the number at the top is 3.
- Dice 6: By the same logic as above, the number at the top is 1.
The sum is 5 + 1 + 5 + 1 + 3 + 1 = 16.
More Chapters | See All...
Inequalities | Pipes and Cisterns | HCF and LCM | Direction Sense Test | Time and Work | Volume and Surface Areas | Matrix Test | Cubes and Dice | Sitting Arrangements | Paper Folding | More...
This Blog Post/Article "Cubes and Dice Quiz Set 07" by Parveen (Hoven) is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Updated on 2020-02-07. Published on: 2016-02-09

